Types de complexité

De manière générale, il faudrait distinguer :

• la complexité dans le meilleur des cas, c’est-à-dire la situation qui génère le moins d’opérations élémentaires ;

• la complexité dans le pire des cas, c’est-à-dire la situation qui génère le plus d’opérations élémentaires (ce sera souvent celle recherchée).

Pour se détacher des contraintes d’implémentation et de matériel, on utilise généralement des ordres de grandeur pour classifier les différentes complexités.

Ordres de grandeur

En notant $T(n)$ le nombre d’opérations élémentaires générées par un algorithme pour une taille $n$ de données, on dit que l’algorithme a pour ordre de grandeur $O \left( f(n) \right)$ s’il existe une constante $C$ telle que $T(n) ≤ C × f(n)$, pour tout entier $n$ à partir d’un certain rang.

Exemples

On reprend les deux algorithmes de la page précédente.
Déterminer leur ordre de grandeur.

1. Algorithme n°1 :

   if n <= 10 :
       n = 3*n
   else:
       n = 2*n
   

   Une réponse

   Nous avons vu qu'il y avait 3 opérations élémentaires dans ce code donc $T(n) = 3 ≤ 3 \times 1$.
   L'algorithme a pour ordre de grandeur O(1).

2. Algorithme n°2 :

   s = 0
   for i in range(1, n+1):
       s = s+i
   

   Une réponse

   Nous avons vu qu'il y avait 3 n + 1 opérations élémentaires dans ce code donc $T(n) = 3 n + 1 ≤ 4 n$ à partir de $n = 1$.
   L'algorithme a pour ordre de grandeur O(n).

Quelques complexités « classiques »

Ordre de grandeur	Type de complexité
O(1)	constante
O( log(n) )	logarithmique
O(n)	linéaire
O( n log(n) )	quasi-linéaire
O(n²)	quadratique
O(2n)	exponentielle

Représentation graphique

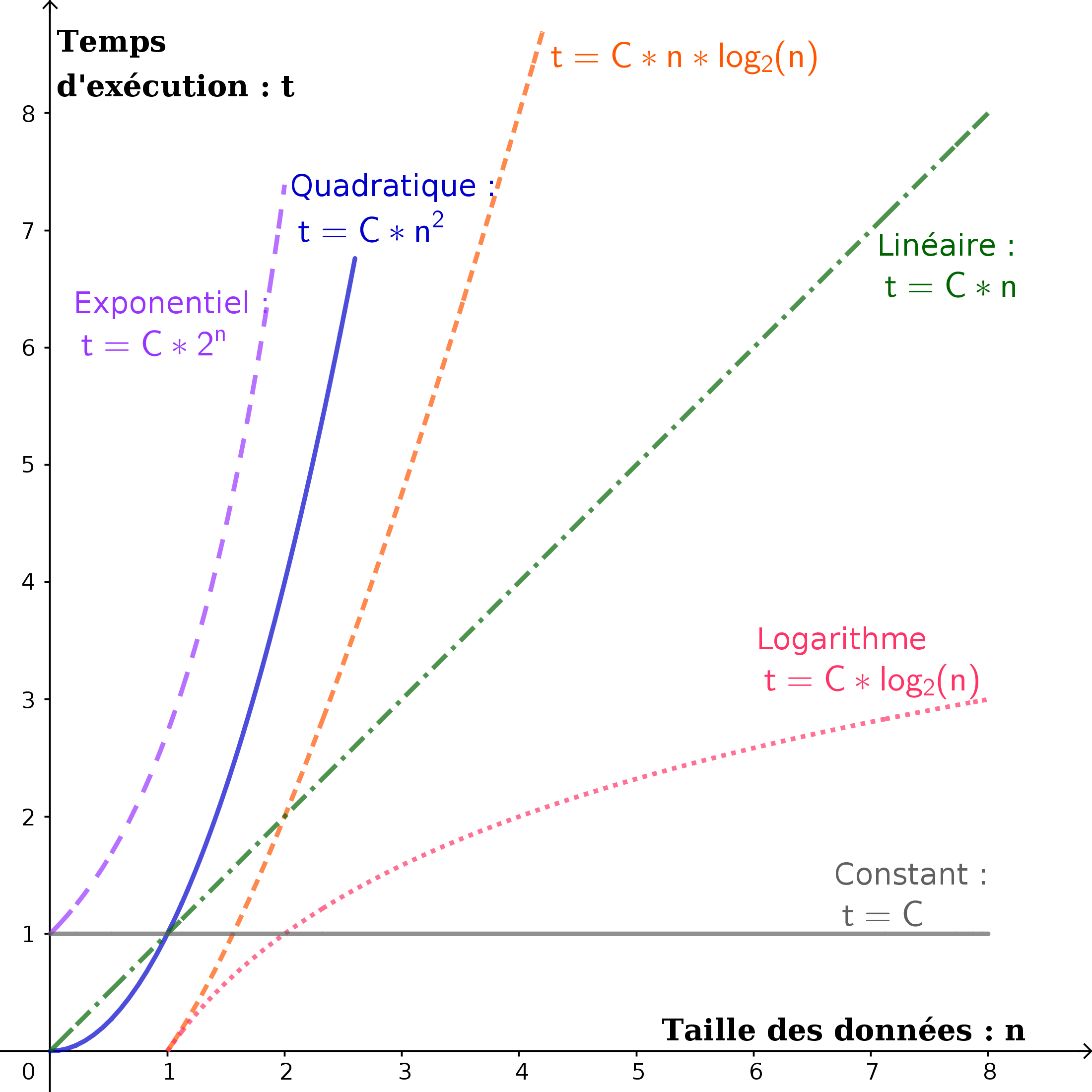
Exemple

On considère l'algorithme suivant, rédigé en Python :

p = 1
i = 1
while i <= n:
    p = p*i
    i = i+1

Déterminer le type de complexité de cet algorithme

Une réponse

Hormis la boucle, toutes les instructions sont des instructions élémentaires. Le type de complexité est donc donné par le nombre de passage dans la boucle.

Puisque i est initialisé à 1 puis incrémenté de 1 à chaque passage dans cette boucle, il faudra n passages dans la boucle pour que i prenne une valeur plus grande que celle de n.
Ces n passages dans la boucle conduisent à une compexité en O(n), soit une complexité linéaire.